Термин "произведение суммы" относится к математическим операциям, сочетающим сложение и умножение. Рассмотрим подробно это понятие и его применение.
Содержание
Основное определение
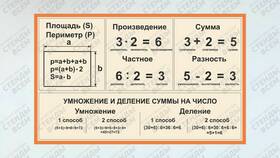
Произведение суммы - это результат умножения суммы двух или более чисел на другой множитель или сумму. В математике это выражается формулой:
| Выражение | Пример |
| (a + b) × c | (2 + 3) × 4 = 20 |
| (a + b) × (c + d) | (1 + 2) × (3 + 4) = 21 |
Дистрибутивный закон
Понятие произведения суммы тесно связано с дистрибутивным законом умножения:
- a × (b + c) = a × b + a × c
- (a + b) × c = a × c + b × c
- (a + b) × (c + d) = a×c + a×d + b×c + b×d
Пример применения
Рассмотрим вычисление (3 + 4) × (5 + 2):
- 3 × 5 = 15
- 3 × 2 = 6
- 4 × 5 = 20
- 4 × 2 = 8
- Сумма: 15 + 6 + 20 + 8 = 49
Применение в алгебре
Произведение сумм широко используется в алгебраических преобразованиях:
| Тип выражения | Пример |
| Квадрат суммы | (a + b)² = a² + 2ab + b² |
| Произведение разности и суммы | (a - b)(a + b) = a² - b² |
Геометрическая интерпретация
Произведение суммы можно представить геометрически:
- Площадь прямоугольника со сторонами (a+b) и (c+d)
- Сумма площадей четырех меньших прямоугольников
Практическое применение
Произведение сумм используется в различных областях:
- Финансовые расчеты (сложные проценты)
- Физика (расчет комбинированных величин)
- Инженерия (расчет нагрузок и сопротивлений)
- Статистика (вычисление дисперсий)
Особые случаи
| Случай | Формула |
| Произведение суммы на 1 | (a + b) × 1 = a + b |
| Произведение суммы на 0 | (a + b) × 0 = 0 |
| Произведение одинаковых сумм | (a + b) × (a + b) = (a + b)² |
Ошибки в вычислениях
При работе с произведением сумм часто допускают ошибки:
- Забывают перемножить все слагаемые
- Путают порядок операций
- Неправильно применяют дистрибутивный закон
- Теряют знаки при работе с отрицательными числами